Aquí les envío la dirección de una página, explica la descomposición Lu y el método de gauss Seidel
http://es.scribd.com/doc/555933/Descomposicion-LU-y-el-Metodo-de-GaussSeidel
viernes, 29 de abril de 2011
mal condicionamiento..
Al resolver un sistema de ecuaciones lineales, es necesario analizar si el resultado calculado es
confiable pues puede ocurrir que los valores obtenidos no tengan la precisión esperada. Un caso
especial se presenta en sistemas que son sensibles a los errores de redondeo introducidos en
los datos y en los cálculos.
Para describir esta situación suponga el siguiente sistema
| 2 3.01 || x 1 || | 5 |
| || ||
| 4 6 || x2 || | 7 |
La solución obtenida con un método directo es:
| 223.25 |
X = | |
|150.00 |
Realicemos un cambio muy pequeño en alguno de los coeficientes del sistema
2 3.01 x 1 5
4.01 6 x2 7
La solución obtenida con el mismo método directo es completamente diferente
127.3894
X
86.3053
continuara...
confiable pues puede ocurrir que los valores obtenidos no tengan la precisión esperada. Un caso
especial se presenta en sistemas que son sensibles a los errores de redondeo introducidos en
los datos y en los cálculos.
Para describir esta situación suponga el siguiente sistema
| 2 3.01 || x 1 || | 5 |
| || ||
| 4 6 || x2 || | 7 |
La solución obtenida con un método directo es:
| 223.25 |
X = | |
|150.00 |
Realicemos un cambio muy pequeño en alguno de los coeficientes del sistema
2 3.01 x 1 5
4.01 6 x2 7
La solución obtenida con el mismo método directo es completamente diferente
127.3894
X
86.3053
continuara...
martes, 26 de abril de 2011
Aplicación de las matrices de Hilbert
Este es una monografía en formato pdf de TEORÍA ESPECTRAL DE OPERADORES EN ESPACIOS DE HILBERT
A modo de curiosidad pueden observar como se pueden aplicar las matrices de hilbert:
link ---- > TEORÍA ESPECTRAL DE OPERADORES EN ESPACIOS DE HILBERT
A modo de curiosidad pueden observar como se pueden aplicar las matrices de hilbert:
link ---- > TEORÍA ESPECTRAL DE OPERADORES EN ESPACIOS DE HILBERT
lunes, 25 de abril de 2011
MATRIZ DE HILBERT
Las matrices de Hilbert se definen de la forma:
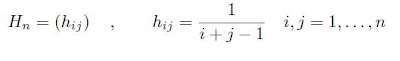
y constituyen un ejemplo de matrices mal condicionadas.

Note que Hn es simétrica para toda n.
Usando la instrucción de MATLAB, hilb(n) podemos generar la matriz de Hilbert de orden n. La instrucción invhilb(n) calcula el inverso exacto de Hn.
Por ejemplo
>>hilb(5)
ans =
1.0000 0.5000 0.3333 0.2500 0.2000
0.5000 0.3333 0.2500 0.2000 0.1667
0.3333 0.2500 0.2000 0.1667 0.1429
0.2500 0.2000 0.1667 0.1429 0.1250
0.2000 0.1667 0.1429 0.1250 0.1111
que es la matriz de Hilbert de orden 5 truncada a cuatro cifras aunque MATLAB guarda más cifras internamente.
Mientras que:
>>invhilb(5)
ans =
25 -300 1050 -1400 630
-300 4800 -18900 26880 -12600
1050 -18900 79380 -117600 56700
-1400 26880 -117600 179200 -88200
630 -12600 56700 -88200 44100
>>invhilb(5)
ans =
25 -300 1050 -1400 630
-300 4800 -18900 26880 -12600
1050 -18900 79380 -117600 56700
-1400 26880 -117600 179200 -88200
630 -12600 56700 -88200 44100
produce el inverso exacto de H5.
Sistemas mal condicionados
Sistemas Mal Condicionados
Algunos sistemas de ecuaciones lineales son extremadamente sensibles a los errores de
redondeo que puedan producirse en el proceso de resolucion. Ya hemos visto en las
secciones anteriores algunos ejemplos, en particular los que podian "arreglarse" mediante
el uso de tecnicas de pivotacion parcial o total. Sin embargo, en determinados casos ni
siquiera el uso de esas tecnicas consiguen llevar a una resolucion precisa, se trata de los
sistemas mal condicionados...
http://campus.usal.es/~mpg/Personales/PersonalMAGL/Docencia/AlgebraTema4Teoria(10-11).pdf
Algunos sistemas de ecuaciones lineales son extremadamente sensibles a los errores de
redondeo que puedan producirse en el proceso de resolucion. Ya hemos visto en las
secciones anteriores algunos ejemplos, en particular los que podian "arreglarse" mediante
el uso de tecnicas de pivotacion parcial o total. Sin embargo, en determinados casos ni
siquiera el uso de esas tecnicas consiguen llevar a una resolucion precisa, se trata de los
sistemas mal condicionados...
http://campus.usal.es/~mpg/Personales/PersonalMAGL/Docencia/AlgebraTema4Teoria(10-11).pdf
Mal Condicionamiento
Aca el enlace a la teoria de Sistemas Mal Condicionados, es un documento en formato pdf.
http://ayudanprimas.com/descargas/icm/analisis-numerico?download=131%3Asistemas-mal-condicionados
http://ayudanprimas.com/descargas/icm/analisis-numerico?download=131%3Asistemas-mal-condicionados
Suscribirse a:
Comentarios (Atom)