MATRIZ DE HILBERT

Las matrices de Hilbert se definen de la forma:

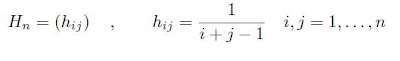
y constituyen un ejemplo de matrices mal condicionadas.

La matriz de Hilbert de orden n se define por:

Note que Hn es simétrica para toda n.

Usando la instrucción de MATLAB, hilb(n) podemos generar la matriz de Hilbert de orden n. La instrucción invhilb(n) calcula el inverso exacto de Hn.

Por ejemplo

>>hilb(5)
ans =
1.0000 0.5000 0.3333 0.2500 0.2000
0.5000 0.3333 0.2500 0.2000 0.1667
0.3333 0.2500 0.2000 0.1667 0.1429
0.2500 0.2000 0.1667 0.1429 0.1250
0.2000 0.1667 0.1429 0.1250 0.1111

que es la matriz de Hilbert de orden 5 truncada a cuatro cifras aunque MATLAB guarda más cifras internamente.

Mientras que:
>>invhilb(5)
ans =
25 -300 1050 -1400 630
-300 4800 -18900 26880 -12600
1050 -18900 79380 -117600 56700
-1400 26880 -117600 179200 -88200
630 -12600 56700 -88200 44100

produce el inverso exacto de H5.