ANALISIS NUMERICO: 6/11/11

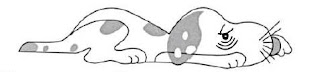
Mediante los trazadores cubicos sujetos vamos a aproximar la parte

superior del perro que se muestra en la siguiente figura . En ella tambien aparece la curva a aproximar en una cuadricula a partir de la cual se construyeron los datos del listado que sigue a la citada figura

Ejecución de un Snoopy en MATLAB.

x1=[1 2 5 6 7 8 10 13 17 ];

y1=[3 3.7 3.9 4.2 5.7 6.6 7.1 6.7 4.5]; %(x1,y1) puntos de la Curva 1

rr1=length(x1);

[CoefP1,P1]=g_sujeto(x1,y1,1,-(2/3)); %P1 polinomio fragmentario de C.1

x2=[17 20.5 22 23 24 25 27 27.7];

y2=[4.5 7.45 6.9 6.1 5.6 5.8 5.4 4.1]; %(x2,y2) puntos de C.2

rr2=length(x2);

[CoefP2,P2]=g_sujeto(x2,y2,2,-4); %P2 polinomio fragmentario de C.2

x3=[27.7 28 29 30];

y3=[4.1 4.3 4.1 3]; %(x3,y3) puntos de C.3

[CoefP3,P3]=g_sujeto(x3,y3,(1/3),-(3/2)); %P3 polinomio fragmentario de C.3

x=[x1(1:(rr1-1)), x2(1:(rr2-1)), x3]; %nodos

y=[y1(1:(rr1-1)), y2(1:(rr2-1)), y3];

Coef=[CoefP1; CoefP2; CoefP3];

P=mkpp(x,Coef); %Polinomio fragmentario total

xp=1:(1/20):30; %discretizacion de [1,30]

yp=ppval(P,xp); %(xp,yp) puntos del trazador

clf

plot(xp,yp)

axis equal

observese como en la de¯nicion del polinomio fragmentario de la segunda curva ponemos el mandato

[CoefP2,P2]=g_sujeto(x2,y2,2,-4)

en lugar de [CoefP2,P2]=g_sujeto(x2,y2,3,-4) y es que creemos que se ajusta mejor al

dibujo una pendiente inicial de magnitud 2 que no de 3.

Ejecutamos ahora las ordenes

Q=polyfit(x,y,length(x)-1);

yp_lag=polyval(Q,xp);

figure(2),

plot(xp,yp_lag)

con el fin de observar las diferencias de realizar una interpolacion fragmentaria y una interpolacion total.

MODELO EMPLEADO:

Para lograr realizar el diseño con splines es necesario enmarcalo en cuadrillas que nos darán las coordenadas requeridas, es decir:

Como se pueden ver se aprecian muchas curvas de esta forma asi que es mejor rotar la imagen a 90 grados hacia el lado izquierdo, teniendose asi coordenadas negativas es decir en el cuadrante 2:

DATOS REQUERIDOS

CODIGO EN C
El código esta hecho en TC versión 3 pero tambien se puede hacer correr en Visual C . Net, se hizo modificaciones al codigo porque el original daba resultados erroneos al encontrar a,b,c y d.

/* trazador cubico*/
#include
#include
#include
double distancia(float a,float);
main()
{ float h[100];
float alfa[100],l[100],m[100],z[100];
float a[100],b[100],c[100],d[100];
float S[100],x,t,intervalo;
int n=2,i;
/* considere que n comineza en 0*/
/* ENTRADA VALORES: Coordenadas (X,Y) */
float X[100]={-1.14,-1.07,-1.05};
float Y[100]={1.16,1.2,1.23};
/* Crear y abrir archivo */
FILE *Resultados;
Resultados = fopen("snoopy[3.5].dat", "w");

/*a contiene los datos de Y*/
for(i=0;i<=n;i++)
{
a[i] = Y[i];

}
/*paso 1*/
for(i=0;i<=n-1;i++)
{ h[i]=X[i+1]-X[i];
/*printf(" %.3f\t \n",h[i]);*/
}
/*paso 2*/
for(i=1;i<=n-1;i++)
{ alfa[i]=((3/h[i])*(a[i+1]-a[i]))-(3/h[i-1])*(a[i]-a[i-1]);
/*printf(" %.3f\t \n",alfa[i]);*/
}
/*paso 3*/
l[0]=1;
m[0]=0;
z[0]=0;
/*paso 4*/
for(i=1;i<=n-1;i++)
{ l[i]=2*(X[i+1]-X[i-1])-h[i-1]*m[i-1];
m[i]=h[i]/l[i];
z[i]=(alfa[i]-h[i-1]*z[i-1])/l[i];
/*printf(" %.5f\t \n",z[i]);*/
}
/*paso 5*/
l[n]=1;
z[n]=0;
c[n]=0;
/*paso 6*/
for(i=(n-1);i>=0;i--)
{ c[i]=z[i]-m[i]*c[i+1];
b[i]=((a[i+1]-a[i])/h[i])-h[i]*(c[i+1]+2*c[i])/3;
d[i]=(c[i+1]-c[i])/(3*h[i]);
/*printf(" %.5f\t \n",d[i]);*/
}

/*generando las coordenadas para el dibujo*/
fprintf(Resultados,"\n# Datos nUm. 1\n# x \t S(x)\n");
/* TItulo del 1er bloque de datos en archivo, corresponde a (x,S(x)) */
/* Creacion de Sj(x) */
for(i=0;i<=n-1;i++)
{ /* Procedimiento para calcular un nUmero de intervalos proporcional
a la distancia entre X[j] y X[j+1]*/
t = 1;
while( ( distancia( X[i+1]-X[i], Y[i+1]-Y[i] )/t ) > 0.01)
/* 0.01 es la distancia deseada entre cada punto a interpolar */
{
t = t + 1;
/* t es el nUmero de trozos en que se divide la distancia entre X[i] y X[j+1] */
}
intervalo = (X[i+1]-X[i]) / t;
/* "intervalo" es la distancia entre cada valor de x a interpolar dentro del intervalo [X[i],X[i+1]] */
x = X[i];
while(x <= X[i+1]) /* Inicio de la interpolaciOn de X[i] a X[i+1] */
{
S[i] = a[i] + b[i]*(x - X[i]) + c[i]*pow((x - X[i]),2) + d[i]*pow((x - X[i]),3);
x = x + intervalo; /* S[i] va tomando valores distintos mientras x aumenta */
/* Paso 9 SALIDA */
fprintf(Resultados," %.5f \t%.5f\n", x, S[i]);
/* Imprime en archivo: (x, S[i](x)) */
}
}
fprintf(Resultados,"\n");
fprintf(Resultados,"\n# Datos nUm. 2\n# x \t\t y\n");
/*fin de generar coordenadas*/

/*mostrando los resultados*/
/* TItulo del 2o bloque de datos en archivo (separado del primero por dos renglones), corresponde a (x,y) */
printf("\n i x a b c d \n");
for(i=0;i<=n-1;i++)
{
printf(" %d %.3f\t %.3f\t %.3f\t %.3f\t %.3f\n",i,X[i],a[i],b[i],c[i],d[i]);
/* Imprime en pantalla x, a, b, c y d, para cada j*/
fprintf(Resultados," %.3f\t %.3f\n",X[i],Y[i]);
/* Imprime en archivo (x,y) para cada i, que son los puntos conocidos al inicio */
}
printf(" %d %.3f\t %.3f\n",i,X[n],a[n]);
fprintf(Resultados," %.3f\t %.3f\n",X[n],Y[n]);
/* Imprime el Ultimo punto (extremo derecho)*/
printf("\n"); /* fin del paso 9 */
/* Cerrar Archivo */
fclose(Resultados);

scanf("%d",i);
}
double distancia(float a, float b)
/* FunciOn que calcula la distancia entre dos puntos:
(x1,y1) y (x2,y2), donde a = x2 -x1, y = y2 - y1 */
{
return( sqrt(pow(a,2) + pow(b,2)) );
}
/* fin del programa */

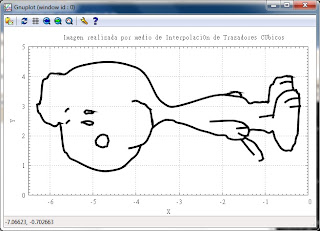
GRAFICADOR GNUPLOT
Este graficador realiza el grafico de forma más rapida, para ello necesitamos el siguiente script al cual le enviamos los archivos con datos de las coordenadas requeridas con el programa hecho en C y le indicamos la siguiente orden: $gnuplot .p

#########################################
# SCRIPT para GNUPLOT, Archivo llamado "snoopy[completo].p"
# para unir todas las partes de la imagen.
# Para activar este postscript escribir en la terminal: gnuplot snoopy[completo].p
# (despues de tener todos los archivos .dat )
##########################################
reset
# poniendo en ceros los sets
set grid
set xlabel "X" # poner etiqueta al eje x
set ylabel "Y" # poner etiqueta al eje y
set title "Imagen realizada por medio de InterpolaciOn de Trazadores CUbicos"
# poner titulo a la grafica
set xrange [-6.5:0] # poner rango eje x [a:b]
set yrange [0:5] # poner rango eje y [a:b]
set xtics 1 # poner graduacion eje x aumentando 1 unidad
set mxtics 10 # poner 10 pequeñas graduaciones entre cada stic
set ytics 1 # poner graduacion eje y aumentando en 1 unidad
set mytics 10 # poner 10 graduaciones entre cada stic
unset key #-0.5,0.5 # posicion del identificador gráfico (deshabilitado)
set style line 1 lt -1 lw 4 #Se define el estilo de línea a utilizar
# DIBUJANDO LA GRAFICA (la figura 5 se dividiO en 25 secciones)
plot "snoopy[1.1].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[1.2].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[1.3].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[1.4].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[1.5].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[1.6].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[1.7].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[1.8].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[1.9].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[2.0].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[2.1].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[2.2].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[2.3].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[2.4].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[2.5].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[2.6].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[2.7].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[2.8].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[2.9].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[3.0].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[3.1].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[3.2].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[3.3].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[3.4].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1, \
"snoopy[3.5].dat" index 0:0 using 1:2 title "S(x)" with lines linestyle 1
# CREANDO UN GRAFICO EN POSTSCRIPT
set terminal png large size 840,697 # gnuplot realiza los ajustes de la salida al tipo
# png antes de salir
set output "snoopy[completo].png" # La salida al fichero.png
replot # volver a graficar
set output # Marca la salida al fichero actual
set terminal pop # pop: es equivalente a “salvar terminal” y “cargar terminal” pero sin
# tener acceso al sistema de ficheros
pause -1 # mantiene la grafica en pantalla hasta que se presione ‘enter’ en la terminal
reset # Regresando los sets a default
quit
# FIN DEL SCRIPT PARA GNUPLOT

RESULTADO

ANALISIS NUMERICO

sábado, 12 de noviembre de 2011

TRABAJO SPLINES

viernes, 11 de noviembre de 2011

Spline Snoopy en Mat Lab ( por Raul Martinez)

POR: QUISPE NELSON FIDEL

function Grafico(x,y,a,b)
h=a:b;
n=length(h);
for i=1:n
j(i)=Spline(x,y,a);
a=a+1;
end

plot(h,j)
end

Snoopy con splines (Maximiliano Ulu)