SNOOPY ( por Winston Quispe)

Aqui les dejo la gráfica completa de Soopy, si les gusta descarguenla de :
http://www.4shared.com/file/--wjUwOD/SNOOPY_Winston_Quispe_Yujra_.html

El Spline Snoopy publicado por Bertha Beatriz Ramos Lequipe

Spline Snoopy

programa
function splinem(mx,my,nk)
m=length(nk);
for z=1:m
for t=1:nk(z)
x(t)=mx(z,t);
y(t)=my(z,t);
end
n=nk(z);

for i=1:n;
a(i)=y(i);
end

for i=1:n-1;
h(i)=x(i+1)-x(i);
end

for i=2:n-1;
alfa(i)=3/h(i)*(a(i+1)-a(i))-3/h(i-1)*(a(i)-a(i-1));
end

l(1)=1;
mu(1)=0;
z(1)=0;

for i=2:n-1;
l(i)=2*(x(i+1)-x(i-1))-h(i-1)*mu(i-1);
mu(i)=h(i)/l(i);
z(i)=(alfa(i)-h(i-1)*z(i-1))/l(i);
end

l(n)=1;
z(n)=0;
c(n)=0;

for i=n-1:-1:1;
c(i)=z(i)-mu(i)*c(i+1);
b(i)=(a(i+1)-a(i))/h(i)-h(i)*(c(i+1)+2*c(i))/3;
d(i)=(c(i+1)-c(i))/(3*h(i));
end

for i=1:n-1;
xf=x(i):0.1:x(i+1);
yf=a(i)+b(i)*(xf-x(i))+c(i)*(xf-x(i)).^2+d(i)*(xf-x(i)).^3;
%if(x(i)<=x0 & x0<=x(i+1))
% y0=y(i)+b(i)*(x0-x(i))+c(i)*((x0-x(i))^2)+d(i)*((x0-x(i))^3);
%end
hold on;
plot(xf,yf,'b');
end

for i=1:n;
hold on;
plot (x(i),y(i),'b','MarkerEdgeColor','r','LineWidth',1);
end
end
p=0:0.1:0.5;
h=p.*20;
plot(p,h,'.');
plot(23,4.6,'.');
end
LA MATRIZ QUE GUARDA LOS DATOS DEL SNOOPY
function [mx,my,nk]=snopyb()
mx(1,:)=[1.3 1.6 2.6 0 0];
mx(2,:)=[2.6 5.1 0 0 0];
mx(3,:)=[5.1 6.2 7.8 11 0];
mx(4,:)=[11 13 15.5 17 0];
mx(5,:)=[17 19 22 23.8 0];
mx(6,:)=[23.8 25.3 28 0 0];
mx(7,:)=[1.3 1.6 2 0 0];
mx(8,:)=[2 7.3 0 0 0];
mx(9,:)=[7.3 8 8.7 0 0];
mx(10,:)=[8 8.4 8.7 0 0];
mx(11,:)=[8 8.9 10.2 11.4 13.1];
mx(12,:)=[13.1 13.4 13.8 0 0];
mx(13,:)=[13.8 14.2 14.6 0 0];
mx(14,:)=[14.6 17.3 0 0 0];
mx(15,:)=[17.3 17.8 18.7 0 0];
mx(16,:)=[18.7 22.4 23.5 0 0];
mx(17,:)=[23.5 23.9 24.1 0 0];
mx(18,:)=[24.1 24.6 25 0 0];
mx(19,:)=[25 26.2 27 27.6 28];
mx(20,:)=[28 28.5 28.8 0 0];
mx(21,:)=[27.6 28.4 28.8 0 0];
mx(22,:)=[27.8 29.2 29.9 0 0];
mx(23,:)=[29.2 29.6 29.9 0 0];
mx(24,:)=[28.8 29.1 29.2 0 0];
mx(25,:)=[28.3 28.7 29.2 0 0];
mx(26,:)=[26.6 28.6 0 0 0];
mx(27,:)=[27 29 0 0 0];
mx(28,:)=[27 28.6 0 0 0];
mx(29,:)=[26.6 28 0 0 0];
mx(30,:)=[26.6 27.8 0 0 0];
mx(31,:)=[24.9 25 25.1 0 0];
mx(32,:)=[23.9 24 24.1 0 0];
mx(33,:)=[23 23.4 23.5 0 0];
mx(34,:)=[19.8 21.6 23.4 24.6 24.9];
mx(35,:)=[17 19 20.6 0 0];
mx(36,:)=[20.2 20.3 20.6 0 0];
mx(37,:)=[20.2 20.4 20.5 0 0];
mx(38,:)=[18.7 19.4 20.2 20.5 0];
mx(39,:)=[17 16.8 16.9 17.3 0];
mx(40,:)=[14.6 14.7 14.8 0 0];
mx(41,:)=[13.6 13.7 13.8 0 0];
mx(42,:)=[12.8 13 13.1 0 0];
mx(43,:)=[11.5 12.7 14 14.8 0];
mx(44,:)=[11.5 11.6 12.1 12.7 0];
mx(45,:)=[11.1 11.2 12.5 12.7 0];
mx(46,:)=[6.2 11.1 12.7 0 0];
mx(47,:)=[22.6 23 23.5 23.8 0];
mx(48,:)=[22.4 22.8 23.5 24.1 0];
mx(49,:)=[22.2 22.9 23.6 24.2 0];
mx(50,:)=[22.4 22.8 23.1 0 0];
mx(51,:)=[22.4 23.2 23.7 0 0];
mx(52,:)=[23.1 23.2 23.3 0 0];
mx(53,:)=[22.6 22.8 23.1 0 0];
mx(54,:)=[15 16.3 16.8 0 0] ;
mx(55,:)=[14.4 14.7 15 0 0];
mx(56,:)=[14.8 14.6 14.4 0 0];




my(1,:)=[3.5 3.8 4 0 0];
my(2,:)=[4 4.1 0 0 0];
my(3,:)=[4.1 4.4 6.1 7.5 0];
my(4,:)=[7.5 7 5.7 5.1 0];
my(5,:)=[5.1 7 7 5.7 0];
my(6,:)=[5.7 5.9 4 0 0];
my(7,:)=[3.5 3.1 3 0 0];
my(8,:)=[3 3.1 0 0 0];
my(9,:)=[3.1 3.3 3.5 0 0];
my(10,:)=[2.4 2.9 3.5 0 0];
my(11,:)=[2.4 1.9 2.1 2.2 1.9];
my(12,:)=[1.9 1.8 1.9 0 0];
my(13,:)=[1.9 1.8 2 0 0];
my(14,:)=[2 2.1 0 0 0];
my(15,:)=[2.1 1.6 1.9 0 0];
my(16,:)=[1.9 1.4 1.5 0 0];
my(17,:)=[1.5 1.4 1.5 0 0];
my(18,:)=[1.5 1.4 1.6 0 0];
my(19,:)=[1.6 1.6 2 2.5 4];
my(20,:)=[4.3 4 3.4 0 0];
my(21,:)=[2.4 2.7 3.4 0 0];
my(22,:)=[4.6 4 3 0 0];
my(23,:)=[2.6 2.7 3 0 0];
my(24,:)=[3.2 2.9 2.6 0 0];
my(25,:)=[2.6 2.4 2.6 0 0];
my(26,:)=[4 5.8 0 0 0];
my(27,:)=[4 5.4 0 0 0];
my(28,:)=[3.5 2.5 0 0 0];
my(29,:)=[3.4 2.1 0 0 0];
my(30,:)=[3 1.8 0 0 0];
my(31,:)=[2.5 2 1.6 0 0];
my(32,:)=[2 1.7 1.5 0 0];
my(33,:)=[1.8 1.6 1.5 0 0];
my(34,:)=[2.8 2.67 2.8 2.9 2.5];
my(35,:)=[4.9 6.6 7 0 0];
my(36,:)=[6 6.6 7 0 0];
my(37,:)=[6 5.5 4.8 0 0];
my(38,:)=[1.9 2.4 3.6 4.8 0];
my(39,:)=[4.9 4.2 2.9 2.1 0];
my(40,:)=[2 2.3 2.7 0 0];
my(41,:)=[2.7 2.4 1.9 0 0];
my(42,:)=[2.6 2.3 1.9 0 0];
my(43,:)=[3.1 3.3 3.2 2.6 0];
my(44,:)=[3.1 3.6 4.1 4.8 0];
my(45,:)=[6.4 6.3 5.7 4.8 0];
my(46,:)=[4.4 6.4 4.8 0 0];
my(47,:)=[4 3.8 3.9 4.4 0];
my(48,:)=[3.8 3.6 3.7 4.2 0];
my(49,:)=[3.6 3.2 3.4 4 0];
my(50,:)=[4.7 5.5 5.6 0 0];
my(51,:)=[4.7 4.9 5.3 0 0];
my(52,:)=[4.3 4.6 4.9 0 0];
my(53,:)=[4.7 4.4 4.3 0 0];
my(54,:)=[4.6 4.4 5.1 0 0];
my(55,:)=[5.1 4.9 4.5 0 0];
my(56,:)=[6 5.6 5.1 0 0];

nk=[3 2 4 4 4 3 3 2 3 3 5 3 3 2 3 3 3 3 5 3 3 3 3 3 3 2 2 2 2 2 3 3 3 5 3 3 3 4 4 3 3 3 4 4 1 3 4 4 4 3 3 3 3 3 3 3];

end

SNOOPY COMPLETO

MILTON MENDOZA CASAS

LO BAJAN POR FAVOR DE LA SIGUIENTE DIRECCION:
http://www.4shared.com/file/-uRy1vOp/156Snoopy.html
SON DOS ARCHIVOS QUE PUEDEN ABRIRLO EN EL MATLAB
EL ARCHIVO snopy.m genera automaticamente los puntos de todos lo spline y esta almecenado estrategicamente en dos matrices mx, my. Es facil!!!
EL ARCHIVO mtspline.m(mx,my,nk) nk es un vector que contiene en cada posicion el numerode datos n, de cada spline del snoopy. Buena suerte!!!

AYUDA: SUBAN ABRAN O HAGAN QUE LOS DOS ARCHIVOS PUEDAN CORRER EN EL MATLAB.
1PASO: Ejecutan lo siguiente: [mx,my,nk]=snopy
2PASO: Ahora dibujen haciendo: mtspline(mx,my,nk)

David Gutierrez

http://www.4shared.com/file/f46VDis5/grafica_del_perrito.html

jhenny laura zegarra spline grafica del perrito

PROGRAMA HECHO POR ALEX SANTOS QUISPE

function Grafico(x,y,a,b)

h=a:b;

n=length(h);

for i=1:n

j(i)=ejemplo(x,y,a);

a=a+1;

end

plot(h,j)

end

%x1=[1,2,5,6,7,8,10,13,17]

%y1=[3,3.7,3.9,4.2,5.7,6.6,7.1,6.7,4.5]

%x2=[17,20,23,24,25,27,27.7]

%y2=[4.5,7,6.1,5.6,5.8,5.2,4.1]

%x3=[27.7,28,29,30]

%y3=[4.1,4.3,4.1,3]

***************************

function [s]=Spline(x,y,x0)

n=length(x);

for i=1:n-1

h(i)=x(i+1)-x(i);

end

%disp(h);

A(1,1)=1;

A(n,n)=1;

for i=2:n-1

A(i,i-1)=h(i-1);

A(i,i)=2*(h(i-1)+h(i));

A(i,i+1)=h(i);

end

%disp(A);

B(1)=0;

B(n)=0;

for i=1:n-2

B(i+1)=(3/h(i+1))*(y(i+2)-y(i+1))-(3/h(i))*(y(i+1)-y(i));

end

c=inv(A)*B';

for i=1:n-1

b(i)=(1/h(i))*(y(i+1)-y(i))-(h(i)/3)*(2*c(i)+c(i+1));

d(i)=(c(i+1)-c(i))/(3*h(i));

end

k=1;

for i=1:n-1

if(x0=x(i))

k=i;

end

end

if(x0>=x(n-1))

k=n-1;

end

end

jhenny laura zegarra

Spline "David Gutierrez"

http://www.4shared.com/file/f46VDis5/grafica_del_perrito.html

Spline SNOOPY - Rolando Quispe Mamani

CODIGO MATLAB 2007
x0=1:0.1:2
x1=2:0.1:5
x2=5:0.1:6
x3=6:0.1:7
x4=7:0.1:8
x5=8:0.1:10
x6=10:0.1:13
x7=13:0.1:17
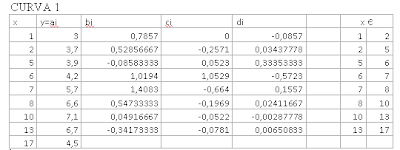
s0=(3)+((0.7857)*(x0-1))+((0)*(x0-1).^2)+((-0.0857)*(x0-1).^3)
s1=(3.7)+((0.5285667)*(x1-2))+((-0.2571)*(x1-2).^2)+((0.034378)*(x1-2).^3)
s2=(3.9)+((-0.08583)*(x2-5))+((0.0523)*(x2-5).^2)+((0.3335333)*(x2-5).^3)
s3=(4.2)+((1.0194)*(x3-6))+((1.0529)*(x3-6).^2)+((-0.5723)*(x3-6).^3)
s4=(5.7)+((1.4083)*(x4-7))+((-0.664)*(x4-7).^2)+((0.1557)*(x4-7).^3)
s5=(6.6)+((0.547333)*(x5-8))+((-0.1969)*(x5-8).^2)+((0.0241167)*(x5-8).^3)
s6=(7.1)+((0.049166)*(x6-10))+((-0.0522)*(x6-10).^2)+((-0.0028778)*(x6-10).^3)
s7=(6.7)+((-0.34173)*(x7-13))+((-0.0781)*(x7-13).^2)+((0.00650833)*(x7-13).^3)

x8=17:0.1:20
x9=20:0.1:23
x10=23:0.1:24
x11=24:0.1:25
x12=25:0.1:27
x13=27:0.1:27.7
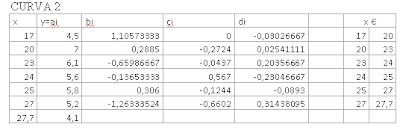
s8=(4.5)+((1.105733)*(x8-17))+((0)*(x8-17).^2)+((-0.0302667)*(x8-17).^3)
s9=(7)+((0.2885)*(x9-20))+((-0.2724)*(x9-20).^2)+((0.0254111111111111)*(x9-20).^3)
s10=(6.1)+((-0.6598667)*(x10-23))+((-0.0437)*(x10-23).^2)+((0.203567)*(x10-23).^3)
s11=(5.6)+((-0.136533)*(x11-24))+((0.567)*(x11-24).^2)+((-0.230467)*(x11-24).^3)
s12=(5.8)+((0.306)*(x12-25))+((-0.1244)*(x12-25).^2)+((-0.0893)*(x12-25).^3)
s13=(5.2)+((-1.26333523809524)*(x13-27))+((-0.6602)*(x13-27).^2)+((0.314380952380953)*(x13-27).^3)

x14=27.7:0.1:28
x15=28:0.1:29
x16=29:0.1:30
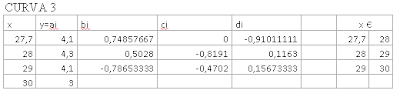
s14=(4.1)+((0.748576)*(x14-27.7))+((0)*(x14-27.7).^2)+((-0.910111)*(x14-27.7).^3)
s15=(4.3)+((0.5028)*(x15-28))+((-0.8191)*(x15-28).^2)+((0.1163)*(x15-28).^3)
s16=(4.1)+((-0.78653)*(x16-29))+((-0.4702)*(x16-29).^2)+((0.15673)*(x16-29).^3)

x17=8:0.1:9
x18=9:0.1:11
x19=11:0.1:19
x20=19:0.1:26
x21=26:0.1:27.2
x22=27.2:0.1:27.7
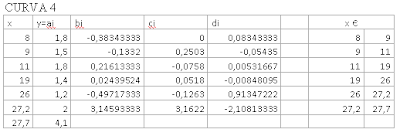
s17=(1.8)+((-0.383433)*(x17-8))+((0)*(x17-8).^2)+((0.083433)*(x17-8).^3)
s18=(1.5)+((-0.1332)*(x18-9))+((0.2503)*(x18-9).^2)+((-0.05435)*(x18-9).^3)
s19=(1.8)+((0.216133)*(x19-11))+((-0.0758)*(x19-11).^2)+((0.00531667)*(x19-11).^3)
s20=(1.4)+((0.0243952380952381)*(x20-19))+((0.0518)*(x20-19).^2)+((-0.00848095238095238)*(x20-19).^3)
s21=(1.2)+((-0.497173)*(x21-26))+((-0.1263)*(x21-26).^2)+((0.9134722)*(x21-26).^3)
s22=(2)+((3.145933)*(x22-27.2))+((3.1622)*(x22-27.2).^2)+((-2.10813)*(x22-27.2).^3)

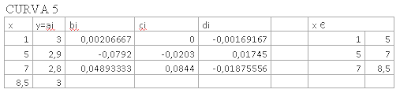
x23=1:0.1:5
x24=5:0.1:7
x25=7:0.1:8.5
s23=(3)+((0.0020666)*(x23-1))+((0)*(x23-1).^2)+((-0.00169167)*(x23-1).^3)
s24=(2.9)+((-0.0792)*(x24-5))+((-0.0203)*(x24-5).^2)+((0.01745)*(x24-5).^3)
s25=(2.8)+((0.048933)*(x25-7))+((0.0844)*(x25-7).^2)+((-0.0187556)*(x25-7).^3)

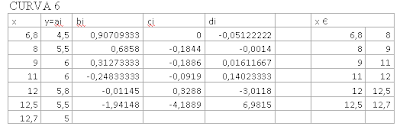
x26=6.8:0.1:8
x27=8:0.1:9
x28=9:0.1:11
x29=11:0.1:12
x30=12:0.1:12.5
x31=12.5:0.1:12.7
s26=(4.5)+((0.907093)*(x26-6.8))+((0)*(x26-6.8).^2)+((-0.05122)*(x26-6.8).^3)
s27=(5.5)+((0.6858)*(x27-8))+((-0.1844)*(x27-8).^2)+((-0.001399)*(x27-8).^3)
s28=(6)+((0.31273)*(x28-9))+((-0.1886)*(x28-9).^2)+((0.01611667)*(x28-9).^3)
s29=(6)+((-0.24833)*(x29-11))+((-0.0919)*(x29-11).^2)+((0.140233)*(x29-11).^3)
s30=(5.8)+((-0.01144)*(x30-12))+((0.3288)*(x30-12).^2)+((-3.0118)*(x30-12).^3)
s31=(5.5)+((-1.94148)*(x31-12.5))+((-4.1889)*(x31-12.5).^2)+((6.981500)*(x31-12.5).^3)

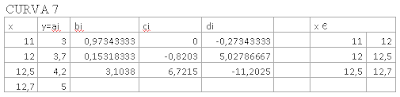
x32=11:0.1:12
x33=12:0.1:12.5
x34=12.5:0.1:12.7
s32=(3)+((0.973433)*(x32-11))+((0)*(x32-11).^2)+((-0.273433)*(x32-11).^3)
s33=(3.7)+((0.1531833)*(x33-12))+((-0.8203)*(x33-12).^2)+((5.0278667)*(x33-12).^3)
s34=(4.2)+((3.103800)*(x34-12.5))+((6.7215)*(x34-12.5).^2)+((-11.2025)*(x34-12.5).^3)

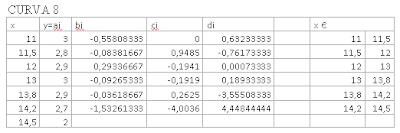
x35=11:0.1:11.5
x36=11.5:0.1:12
x37=12:0.1:13
x38=13:0.1:13.8
x39=13.8:0.1:14.2
x40=14.2:0.1:14.5
s35=(3)+((-0.5580833)*(x35-11))+((0)*(x35-11).^2)+((0.63233)*(x35-11).^3)
s36=(2.8)+((-0.0838166)*(x36-11.5))+((0.9485)*(x36-11.5).^2)+((-0.761733)*(x36-11.5).^3)
s37=(2.9)+((0.2933667)*(x37-12))+((-0.1941)*(x37-12).^2)+((0.0007333)*(x37-12).^3)
s38=(3)+((-0.0926533)*(x38-13))+((-0.1919)*(x38-13).^2)+((0.18933)*(x38-13).^3)
s39=(2.9)+((-0.0361866)*(x39-13.8))+((0.2625)*(x39-13.8).^2)+((-3.555083335)*(x39-13.8).^3)
s40=(2.7)+((-1.5326133)*(x40-14.2))+((-4.0036)*(x40-14.2).^2)+((4.44844444)*(x40-14.2).^3)

x41=15.5:0.1:16
x42=16:0.1:17
x43=17:0.1:19
x44=19:0.1:22
x45=22:0.1:24.5
x46=24.5:0.1:25
s41=(1.5)+((2.0978167)*(x41-15.5))+((0)*(x41-15.5).^2)+((-1.191267)*(x41-15.5).^3)
s42=(2.4)+((1.20433)*(x42-16))+((-1.7869)*(x42-16).^2)+((0.682567)*(x42-16).^3)
s43=(2.5)+((-0.321867)*(x43-17))+((0.2608)*(x43-17).^2)+((-0.062433)*(x43-17).^3)
s44=(2.4)+((-0.0279666666666666)*(x44-19))+((-0.1138)*(x44-19).^2)+((0.03363)*(x44-19).^3)
s45=(2.2)+((0.1974167)*(x45-22))+((0.1889)*(x45-22).^2)+((-0.0943467)*(x45-22).^3)
s46=(2.4)+((-0.6271)*(x46-24.5))+((-0.5187)*(x46-24.5).^2)+((0.3458)*(x46-24.5).^3)


plot(x0,s0,'k','LineWidth',2);grid;title('Grafico');hold on;
plot(x0,s0,'k','LineWidth',2);
plot(x1,s1,'k','LineWidth',2);
plot(x2,s2,'k','LineWidth',2);
plot(x3,s3,'k','LineWidth',2);
plot(x4,s4,'k','LineWidth',2);
plot(x5,s5,'k','LineWidth',2);
plot(x6,s6,'k','LineWidth',2);
plot(x7,s7,'k','LineWidth',2);

plot(x8,s8,'r','LineWidth',2);
plot(x9,s9,'r','LineWidth',2);
plot(x10,s10,'r','LineWidth',2);
plot(x11,s11,'r','LineWidth',2);
plot(x12,s12,'r','LineWidth',2);
plot(x13,s13,'r','LineWidth',2);

plot(x14,s14,'g','LineWidth',2);
plot(x15,s15,'g','LineWidth',2);
plot(x16,s16,'g','LineWidth',2);

plot(x17,s17,'k','LineWidth',2);
plot(x18,s18,'k','LineWidth',2);
plot(x19,s19,'k','LineWidth',2);
plot(x20,s20,'k','LineWidth',2);
plot(x21,s21,'k','LineWidth',2);
plot(x22,s22,'k','LineWidth',2);

plot(x23,s23,'b','LineWidth',2);
plot(x24,s24,'b','LineWidth',2);
plot(x25,s25,'b','LineWidth',2);

plot(x26,s26,'k','LineWidth',2);
plot(x27,s27,'k','LineWidth',2);
plot(x28,s28,'k','LineWidth',2);
plot(x29,s29,'k','LineWidth',2);
plot(x30,s30,'k','LineWidth',2);
plot(x31,s31,'k','LineWidth',2);

plot(x32,s32,'r','LineWidth',2);
plot(x33,s33,'r','LineWidth',2);
plot(x34,s34,'r','LineWidth',2);

plot(x35,s35,'k','LineWidth',2);
plot(x36,s36,'k','LineWidth',2);
plot(x37,s37,'k','LineWidth',2);
plot(x38,s38,'k','LineWidth',2);
plot(x39,s39,'k','LineWidth',2);
plot(x40,s40,'k','LineWidth',2);

plot(x41,s41,'b','LineWidth',2);
plot(x42,s42,'b','LineWidth',2);
plot(x43,s43,'b','LineWidth',2);
plot(x44,s44,'b','LineWidth',2);
plot(x45,s45,'b','LineWidth',2);
plot(x46,s46,'b','LineWidth',2);

hold off;